Présentation
L'informatique est un élément essentiel de la recherche scientifique. Les problèmes mathématiques, d'ingénierie, scientifiques et autres problèmes techniques sont complexes et nécessitent une puissance et une rapidité de calcul. Python fournit la bibliothèque SciPy pour résoudre les problèmes techniques par calcul.
Cet article présente un didacticiel SciPy et explique comment implémenter le code en Python avec des exemples.

Prérequis
- Python 2.7 ou Python 3 installé
- Un environnement Python pour exécuter le code.
- Bibliothèque SciPy installée.
- Bibliothèque NumPy installée (Suivez notre guide :Comment installer NumPy).
- Bibliothèque Matplotlib installée pour le traçage (facultatif).
Qu'est-ce que SciPy ?
SciPy (Sci entifique Py thon) est un module de calcul scientifique open-source pour Python. Basé sur NumPy, SciPy inclut des outils pour résoudre des problèmes scientifiques. Les scientifiques ont créé cette bibliothèque pour répondre à leurs besoins croissants en matière de résolution de problèmes complexes.
SciPy contre NumPy
La librairie NumPy (Num Eric Py thon) fait du calcul numérique. Les scientifiques utilisent cette bibliothèque pour travailler avec des tableaux puisque NumPy couvre les utilisations élémentaires en science des données, en statistiques et en mathématiques.
SciPy couvre les calculs et fonctions avancés. Cette bibliothèque ajoute plus de fonctionnalités de science des données, toutes les fonctions d'algèbre linéaire et des algorithmes scientifiques standard.
Pourquoi utiliser SciPy ?
La bibliothèque SciPy s'appuie sur NumPy et fonctionne sur des tableaux. La puissance de calcul est rapide car NumPy utilise C pour l'évaluation.
La pile scientifique Python est similaire à MATLAB, Octave, Scilab et Fortran. La principale différence est que Python est facile à apprendre et à écrire.
Sous-packages SciPy
La bibliothèque SciPy a différents groupes de sous-packages. Il existe deux manières d'importer des sous-packages depuis le module SciPy :
import scipy.<sub package name> as <alias>Ou alternativement :
from scipy import <sub package name> as <alias>Dans les deux méthodes d'importation, l'alias est facultatif.
Fonctions SciPy
SciPy inclut de nombreuses fonctions de tableau principales disponibles dans NumPy et certains des modules couramment utilisés des sous-paquetages SciPy.
Pour importer une fonction à partir d'un sous-package, utilisez :
from scipy.<subpackage> import <function>Fonctions de base
Pour obtenir de l'aide et des informations sur n'importe quelle fonction SciPy, utilisez help() commande :
help(<name of function>)
Le help() La commande n'a pas besoin de paramètres. Après l'exécution sans paramètres, une invite apparaît lorsque vous saisissez le nom de la fonction.
Un autre moyen rapide d'obtenir de l'aide avec n'importe quelle commande en Python consiste à écrire le nom de la commande, à mettre un point d'interrogation à la fin et à exécuter le code.
Fonctions spéciales
Les fonctions spéciales du module SciPy incluent des calculs et des algorithmes couramment utilisés. Toutes les fonctions spéciales acceptent les tableaux NumPy en entrée. Les calculs sont élémentaires.
Pour importer le special sous-package, utilisez :
import scipy.special as specialOu alternativement :
from scipy import special
Pour importer une fonction spécifique depuis le special sous-package, utilisez :
from scipy.special import <function name>Factoriel
Évaluez la factorielle de n'importe quel nombre en exécutant :
special.factorial(<integer or array>)Par exemple, pour trouver la factorielle de dix, utilisez :
special.factorial(10)
Permutations et combinaisons
Pour trouver le nombre de permutations, utilisez :
special.perm(<number of elements>, <number of elements taken>)Par exemple, pour voir le nombre de permutations de trois éléments pris deux à la fois :
special.perm(6,2)
De même, trouvez le nombre de combinaisons avec :
special.comb(<number of elements>, <number of elements taken>, repetition=<True or False>)Pour trouver le nombre de combinaisons de trois éléments pris deux à deux avec répétition, saisissez :
special.comb(6,2, repetition=True)
Les permutations et les combinaisons sont utilisées dans les algorithmes de tri en informatique.
Fonctions exponentielles
Les fonctions exponentielles évaluent les exposants pour différentes bases.
Calculez les exposants de la base dix avec :
special.exp10(<integer or array>)Par exemple :
special.exp10([0,1,2])
L'informatique utilise souvent des fonctions exponentielles de base deux :
special.exp2(<integer or array>)Calculez la puissance dixième de la base deux avec :
special.exp2(10)
Somme logarithmique des exponentielles
La somme logarithmique des exponentielles (LSE ou LogSumExp) est une approximation utilisée par les algorithmes d'apprentissage automatique. Calculez le LSE avec :
special.logsumexp(<integer or array>)
Fonction de Bessel
Les fonctions de Bessel apparaissent dans la propagation des ondes, le traitement du signal et les problèmes de potentiel statique. Trouvez la fonction de Bessel de première espèce avec :
special.jn(<integer order>, <integer or array>)Profitez de la pile complète pour visualiser la fonction de Bessel. Pour trouver la fonction de Bessel du second ordre du premier type, utilisez :
#import stack
import scipy.special as special
import matplotlib.pyplot as plt
import numpy as np
#The X-axis
x = np.linspace(1,50,100)
#Bessel function of the first kind order two
jn1 = special.jn(2,x)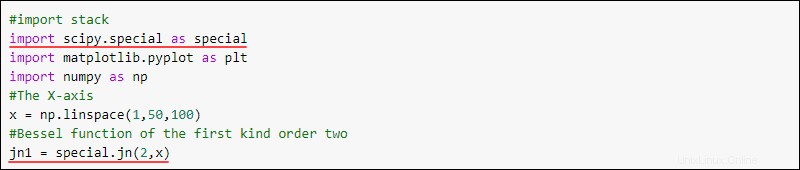
Tracez les résultats :
#Plotting
plt.title('Bessel function first kind order two')
plt.plot(x, jn1)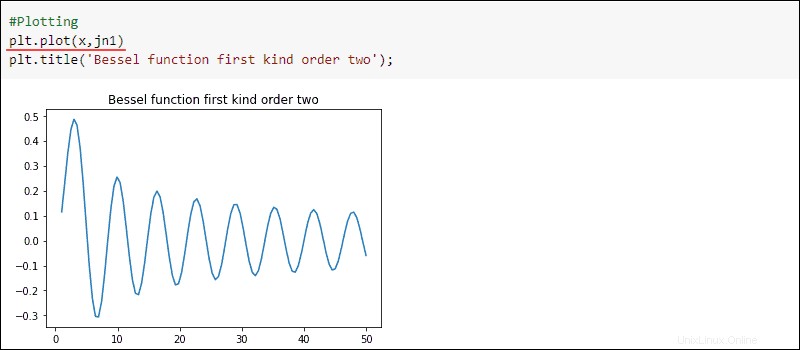
Fonctions d'intégration et ODE
SciPy fournit un sous-package pour les calculs avec des intégrales définies. Pour importer l'integrate sous-package, utilisez :
import scipy.integrate as integrateOu alternativement :
from scipy import integrate
Importer une fonction spécifique du sous-package integrate avec :
from scipy.integrate import <function name>Intégration générale
Calculer une seule variable intégrale avec le quad fonction de integrate sous-package :
integrate.quad(<function>, <lower limit>, <upper limit>)
La function l'entrée est définie à l'aide d'une fonction lambda.
Par exemple, pour calculer l'intégrale définie de la fonction x+1 entre zéro et un :
from scipy import integrate
f = lambda x: x+1
integrate.quad(f, 0, 1)La sortie affiche deux valeurs. La première valeur est l'intégrale évaluée et la seconde est l'erreur d'estimation.

Fonctions d'optimisation
SciPy a un sous-package d'optimisation pour trouver le minimum ou le maximum d'une fonction. Le optimize le sous-package comprend des solveurs et des algorithmes pour trouver des valeurs optimales locales et globales.
Pour importer le sous-package d'optimisation :
from scipy import optimizeOu utilisez :
import scipy.optimize as optimize
Pour importer une fonction spécifique du sous-package optimize , exécutez :
from scipy.optimize import <function name>Réduire une fonction
Trouver un minimum d'une fonction est utilisé dans l'apprentissage automatique pour réduire la perte (ou l'erreur) d'un algorithme.
Par exemple, vous pouvez créer une fonction et trouver le minimum. Pour ce faire, utilisez le fmin fonction de optimize sous-package dans SciPy :
#Import stack
import numpy as np
from scipy import optimize
#Defining inverse sine function
def f(x):
return -np.sin(x)
#X-axis
x = np.linspace(0,5,100)
#Starting point
start = 3
#Simplex algorithm for optimization
optimized = optimize.fmin(f,start)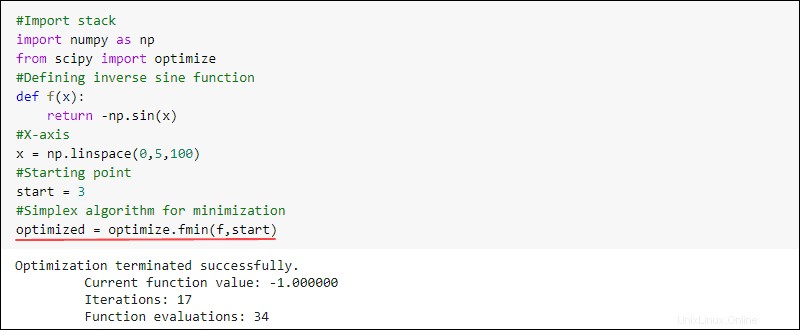
Pour tracer le résultat, exécutez :
import matplotlib.pyplot as plt
plt.plot(x, f(x))
plt.scatter(start,f(start))
plt.scatter(optimized, f(optimized))
plt.legend(['Function -sin(x)', 'Starting point', 'Optimized minimum'])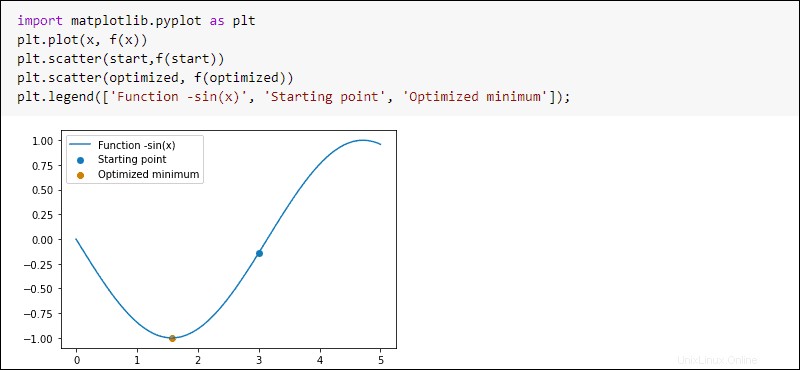
Fonctions de transformation de Fourier
SciPy inclut un sous-package pour les fonctions de transformation de Fourier appelé fftpack . Les transformations sont des transformations discrètes de Fourier (DFT). Toutes les transformations sont appliquées à l'aide de l'algorithme Fast Fourier Transformation (FFT).
Pour importer le fftpack sous-package, utilisez :
import scipy.fftpack as fftpackOu :
from scipy import fftpackTransformée de Fourier rapide
Par exemple, créez une fonction périodique comme somme de trois ondes sinusoïdales :
import numpy as np
freq_samp = 100
#Time
t = np.linspace(0, 1, freq_samp*2, endpoint = False )
#Frequencies
f1, f2, f3 = 1, 5, 20
#Amplitudes
A1, A2, A3 = 3, 2, 1
x1 = A1*np.sin(f1*2*np.pi*t)
x2 = A2*np.sin(f2*2*np.pi*t)
x3 = A3*np.sin(f3*2*np.pi*t)
#Sum of waves
x = x1+x2+x3
Tracez les vagues en utilisant matplotlib :
import matplotlib.pyplot as plt
plt.subplot(2,1,1)
plt.plot(t,x1,t,x2,t,x3)
plt.subplot(2,1,2)
plt.plot(t,x)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');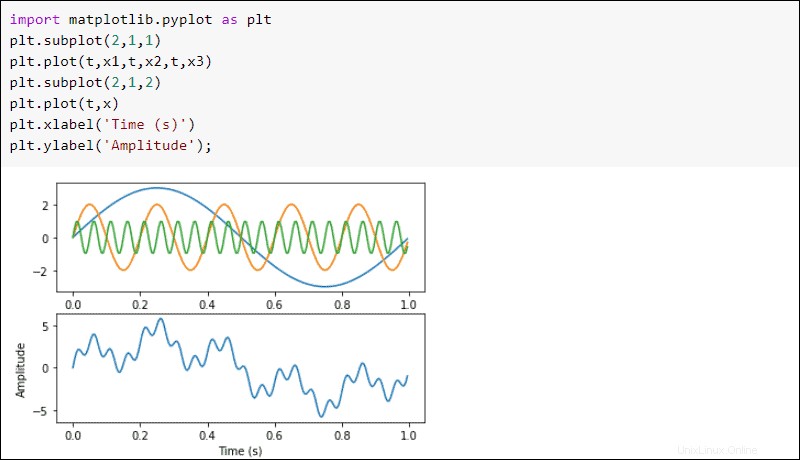
Ensuite, appliquez le fft et fftfreq fonctions du fftpack pour faire une transformée de Fourier du signal.
from scipy import fftpack
A = fftpack.fft(x)
freq = fftpack.fftfreq(len(x))*freq_samp*2
Tracez les résultats pour voir le domaine fréquentiel :
plt.stem(freq,np.abs(A)/freq_samp,use_line_collection=True)
plt.xlim(-25,25)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()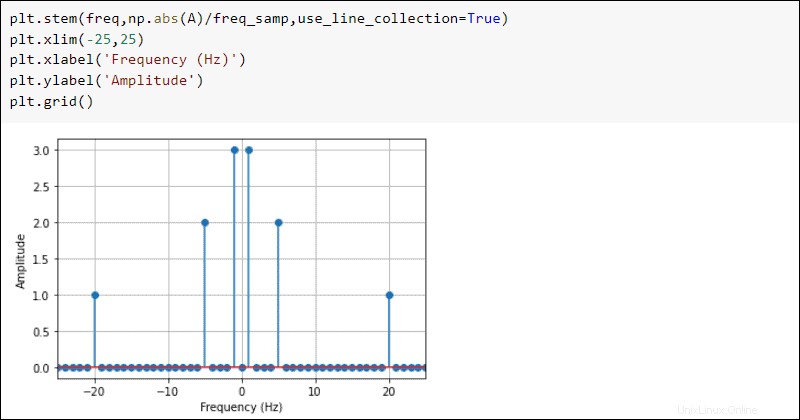
Fonctions de traitement du signal
Le sous-paquetage signal comprend des fonctions utilisées dans le traitement du signal. Pour importer le signal , exécutez :
import scipy.signal as signalOu alternativement :
from scipy import signalConvolution
Une tâche courante dans le traitement du signal est la convolution. Le sous-package SciPy signal a la fonction convolve pour effectuer cette tâche. Par exemple, créez deux signaux avec des fréquences différentes :
import numpy as np
#Time
t = np.linspace(0,1,100)
#Frequency
f1, f2 = 5, 2
#Two signals of different frequencies
first_signal = np.sin(f1*2*np.pi*t)
second_signal = np.sin(f2*2*np.pi*t)
Tracez les signaux :
import matplotlib.pyplot as plt
#Plotting both signals
plt.subplot(2,1,1)
plt.plot(t, first_signal)
plt.subplot(2,1,2)
plt.plot(t, second_signal)
plt.ylabel('Amplitude')
plt.xlabel('Time (s)')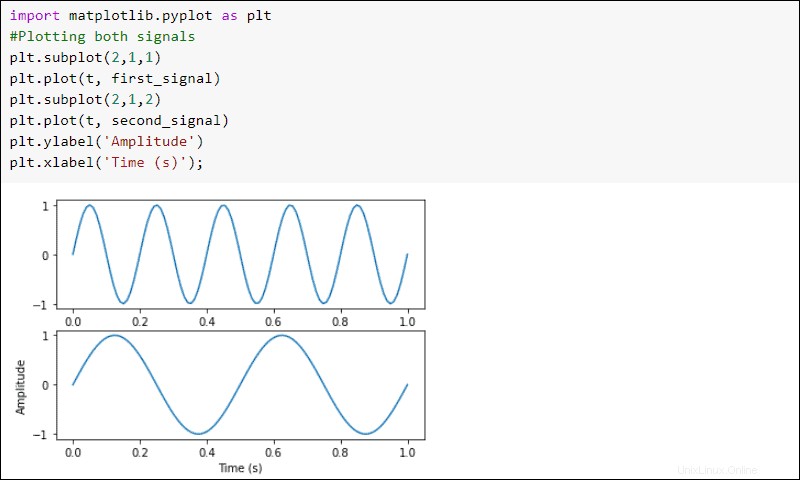
Importer le signal sous-paquet de scipy . Utilisez la convolve fonction à partir du signal sous-package pour convoluer les deux signaux :
#Importing the signal subpackage
from scipy import signal
#Convolving two signals
convolution = signal.convolve(first_signal, second_signal, mode='same')
Tracez les résultats :
#Plotting the result
plt.plot(t, convolution)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')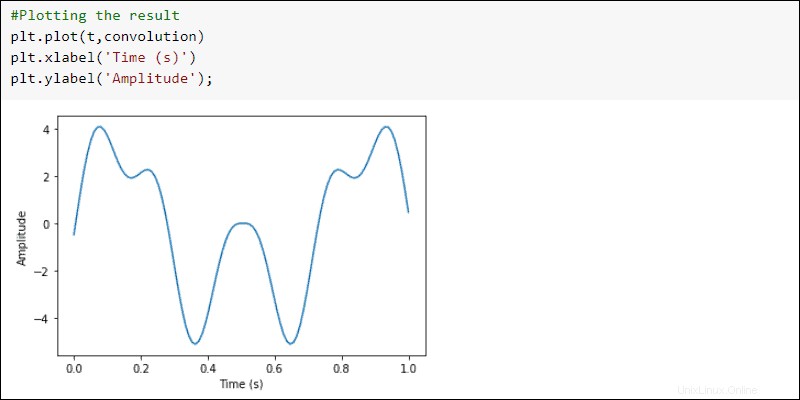
Fonctions d'interpolation
L'interpolation est utilisée dans le domaine de l'analyse numérique pour généraliser les valeurs entre deux points. SciPy a le interpolate sous-package avec fonctions et algorithmes d'interpolation.
Importer l'interpolate sous-package avec :
import scipy.interpolate as interpolateOu :
from scipy import interpolateInterpolation unidimensionnelle
L'interpolate SciPy le sous-paquet a le interp1d fonction d'interpolation unidimensionnelle des données. Par exemple, créez jouet données en utilisant numpy :
import numpy as np
#Create toy data
x = np.arange(0,10,0.5)
y = np.sin(x)
Interpoler les données avec interp1d à partir de l'interpolate sous-package :
from scipy import interpolate
#Interpolate
f = interpolate.interp1d(x, y)
#Create interpolation function
x_i = np.arange(0,10,3)
y_i = f(x_i)
Tracez les résultats :
#Plot results
plt.scatter(x,y)
plt.plot(x_i, y_i)
plt.legend(['Interpolation', 'Data points'])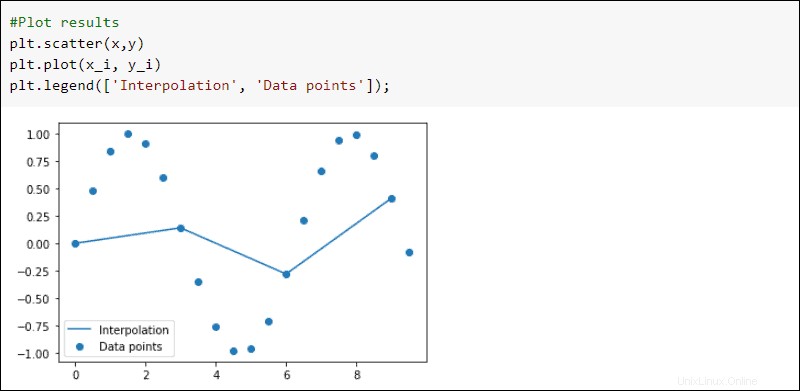
Algèbre linéaire
SciPy a un sous-package d'algèbre linéaire complet. Le sous-package d'algèbre linéaire SciPy est optimisé avec les bibliothèques ATLAS LAPACK et BLAS pour un calcul plus rapide.
Pour importer le package d'algèbre linéaire depuis SciPy, exécutez :
import scipy.linalg as linalgOu utilisez :
from scipy import linalgToutes les fonctions d'algèbre linéaire attendent un tableau NumPy en entrée.
Déterminant
Calculer le déterminant d'une matrice avec det du linalg sous-package :
linalg.det(<numpy array>)Par exemple :
import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the determinant
linalg.det(A)
Matrice inverse
Déterminer la matrice inverse en utilisant inv :
linalg.inv(<numpy array>)Par exemple :
import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3,4]])
from scipy import linalg
#Calculate the inverse matrix
linalg.inv(A)
Vecteurs propres et valeurs propres
Les vecteurs propres et les valeurs propres sont une méthode de décomposition matricielle. Le problème valeur propre-vecteur propre est un problème d'algèbre linéaire couramment mis en œuvre.
Le eig la fonction trouve les valeurs propres et les vecteurs propres d'une matrice :
linalg.eig(<numpy array>)La sortie renvoie deux tableaux. Le premier contient des valeurs propres et le second des vecteurs propres pour la matrice donnée. Par exemple :
import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the eigenvalues and eigenvectors
linalg.eig(A)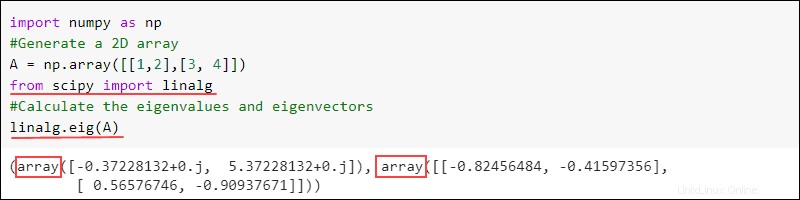
Structures de données spatiales et algorithmes
Les structures de données spatiales sont des objets constitués de points, de lignes et de surfaces. SciPy dispose d'algorithmes pour les structures de données spatiales puisqu'ils s'appliquent à de nombreuses disciplines scientifiques.
Importer le spatial sous-package de SciPy avec :
import scipy.spatial as spatialOu :
from scipy import spatialUn exemple notable d'algorithme spatial est le diagramme de Voronoi. Pour un ensemble de points donné, les cartes de Voronoi divisent un plan en régions. Si un nouveau point tombe dans une région, le point de la région est le voisin le plus proche.
Par exemple, créez un diagramme de Voronoi à partir de vingt points aléatoires :
from scipy.spatial import Voronoi
import numpy as np
points = np.random.rand(20,2)
voronoi = Voronoi(points)
from scipy.spatial import voronoi_plot_2d
fig = voronoi_plot_2d(voronoi,show_vertices=False)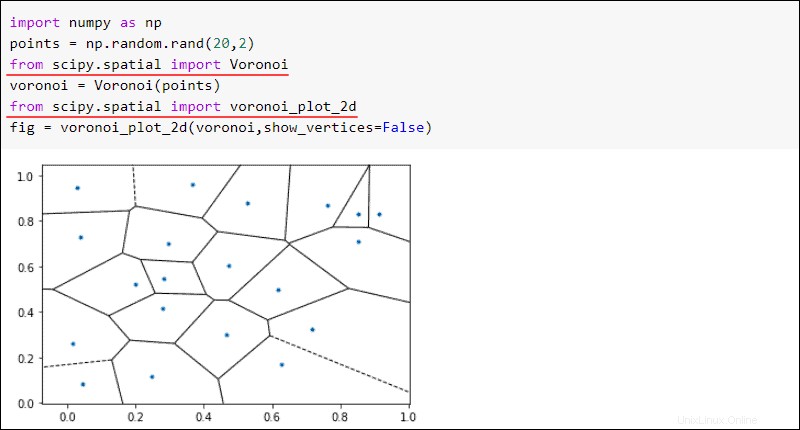
Traitement des images
SciPy a un sous-package pour divers traitements d'images à n dimensions. Pour importer la ndimage sous-package, exécutez :
import scipy.ndimage as ndimageOu utilisez :
from scipy import ndimage
Le SciPy misc le sous-paquet contient un exemple d'image à des fins de démonstration. Pour importer le misc sous-paquetage et affichez l'image :
from scipy import misc
from matplotlib import pyplot as plt
raccoon = misc.face()
#show image
plt.imshow(raccoon)
plt.show()
Importer le ndimage sous-package et appliquez un uniform_filter à l'image. Affichez l'image pour voir les résultats :
from scipy import ndimage
filtered = ndimage.uniform_filter(raccoon)
plt.imshow(filtered)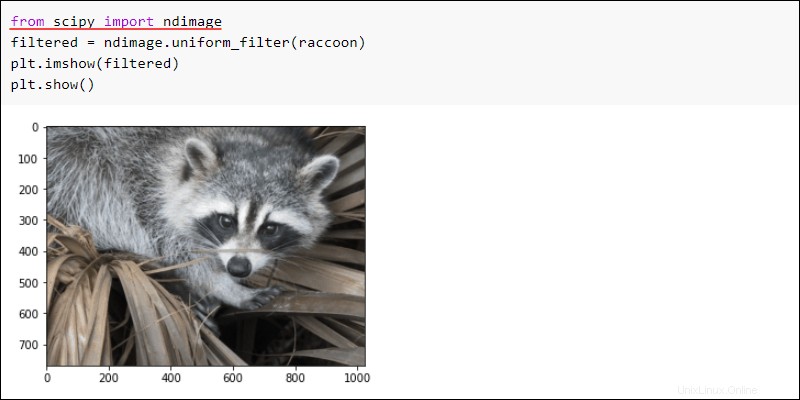
Fichier IO (paquet d'entrée/sortie de fichier)
SciPy a un sous-package d'entrée et de sortie de fichier appelé io . Le io le sous-paquetage est utilisé pour lire et écrire des formats de données à partir de différents programmes et langages de calcul scientifique, tels que Fortran, MATLAB, IDL, etc.
Importer le io sous-package de SciPy avec :
import scipy.io as sioOu utilisez :
from scipy import io as sio