Si votre objectif est d'utiliser un profileur, utilisez l'un de ceux suggérés.
Cependant, si vous êtes pressé et que vous pouvez interrompre manuellement votre programme sous le débogueur alors qu'il est subjectivement lent, il existe un moyen simple de détecter les problèmes de performances.
Il suffit de l'arrêter plusieurs fois et de regarder à chaque fois la pile d'appels. S'il y a un code qui perd un certain pourcentage du temps, 20% ou 50% ou autre, c'est la probabilité que vous l'attrapiez en flagrant délit sur chaque échantillon. Donc, c'est à peu près le pourcentage d'échantillons sur lesquels vous le verrez. Aucune conjecture éclairée n'est requise. Si vous devinez quel est le problème, cela le prouvera ou le réfutera.
Vous pouvez avoir plusieurs problèmes de performances de tailles différentes. Si vous nettoyez l'un d'entre eux, les autres prendront un pourcentage plus élevé et seront plus faciles à repérer lors des passages suivants. Cet effet de grossissement , lorsqu'il est aggravé par plusieurs problèmes, peut entraîner des facteurs d'accélération vraiment massifs.
Mise en garde :Les programmeurs ont tendance à être sceptiques à l'égard de cette technique à moins qu'ils ne l'aient utilisée eux-mêmes. Ils diront que les profileurs vous donnent ces informations, mais ce n'est vrai que s'ils échantillonnent l'ensemble de la pile d'appels, puis vous permettent d'examiner un ensemble aléatoire d'échantillons. (Les résumés sont là où les informations sont perdues.) Les graphiques d'appels ne vous donnent pas les mêmes informations, car
- Ils ne résument pas au niveau de l'instruction, et
- Ils donnent des résumés déroutants en présence de récursivité.
Ils diront également que cela ne fonctionne que sur les programmes jouets, alors qu'en réalité cela fonctionne sur n'importe quel programme, et cela semble mieux fonctionner sur les programmes plus importants, car ils ont tendance à avoir plus de problèmes à trouver. Ils diront qu'il trouve parfois des choses qui ne sont pas des problèmes, mais ce n'est vrai que si vous voyez quelque chose une fois . Si vous voyez un problème sur plus d'un échantillon, c'est réel.
P.S. Cela peut également être fait sur des programmes multi-thread s'il existe un moyen de collecter des échantillons de pile d'appels du pool de threads à un moment donné, comme c'est le cas en Java.
P.P.S En règle générale, plus vous avez de couches d'abstraction dans votre logiciel, plus vous avez de chances de trouver que c'est la cause des problèmes de performances (et la possibilité d'accélérer).
Ajouté :Ce n'est peut-être pas évident, mais la technique d'échantillonnage de pile fonctionne aussi bien en présence de récursivité. La raison en est que le temps qui serait économisé par la suppression d'une instruction est approximé par la fraction d'échantillons la contenant, quel que soit le nombre de fois qu'elle peut se produire dans un échantillon.
Une autre objection que j'entends souvent est :"Cela s'arrêtera quelque part au hasard, et cela passera à côté du vrai problème ". Cela vient du fait d'avoir une idée préalable de ce qu'est le véritable problème. Une propriété clé des problèmes de performance est qu'ils défient les attentes. L'échantillonnage vous indique que quelque chose est un problème et votre première réaction est l'incrédulité. C'est naturel, mais vous pouvez assurez-vous que s'il trouve un problème, il est réel, et vice-versa.
Ajouté :Permettez-moi de faire une explication bayésienne de la façon dont cela fonctionne. Supposons qu'il existe une instruction I (appel ou autre) qui est sur la pile d'appels une fraction f du temps (et donc coûte autant). Pour simplifier, supposons que nous ne sachions pas ce que f est, mais supposons que c'est soit 0,1, 0,2, 0,3, ... 0,9, 1,0, et que la probabilité a priori de chacune de ces possibilités soit de 0,1, donc tous ces coûts sont également probables a priori.
Supposons ensuite que nous ne prenions que 2 échantillons de pile et que nous voyions l'instruction I sur les deux échantillons, observation désignée o=2/2 . Cela nous donne de nouvelles estimations de la fréquence f de I , d'après ceci :
Prior
P(f=x) x P(o=2/2|f=x) P(o=2/2&&f=x) P(o=2/2&&f >= x) P(f >= x | o=2/2)
0.1 1 1 0.1 0.1 0.25974026
0.1 0.9 0.81 0.081 0.181 0.47012987
0.1 0.8 0.64 0.064 0.245 0.636363636
0.1 0.7 0.49 0.049 0.294 0.763636364
0.1 0.6 0.36 0.036 0.33 0.857142857
0.1 0.5 0.25 0.025 0.355 0.922077922
0.1 0.4 0.16 0.016 0.371 0.963636364
0.1 0.3 0.09 0.009 0.38 0.987012987
0.1 0.2 0.04 0.004 0.384 0.997402597
0.1 0.1 0.01 0.001 0.385 1
P(o=2/2) 0.385
La dernière colonne indique que, par exemple, la probabilité que f>= 0,5 correspond à 92 %, en hausse par rapport à l'hypothèse précédente de 60 %.
Supposons que les hypothèses a priori soient différentes. Supposons que nous supposons P(f=0.1) est de 0,991 (presque certain) et toutes les autres possibilités sont presque impossibles (0,001). En d'autres termes, notre certitude préalable est que I Est bon marché. Alors on obtient :
Prior
P(f=x) x P(o=2/2|f=x) P(o=2/2&& f=x) P(o=2/2&&f >= x) P(f >= x | o=2/2)
0.001 1 1 0.001 0.001 0.072727273
0.001 0.9 0.81 0.00081 0.00181 0.131636364
0.001 0.8 0.64 0.00064 0.00245 0.178181818
0.001 0.7 0.49 0.00049 0.00294 0.213818182
0.001 0.6 0.36 0.00036 0.0033 0.24
0.001 0.5 0.25 0.00025 0.00355 0.258181818
0.001 0.4 0.16 0.00016 0.00371 0.269818182
0.001 0.3 0.09 0.00009 0.0038 0.276363636
0.001 0.2 0.04 0.00004 0.00384 0.279272727
0.991 0.1 0.01 0.00991 0.01375 1
P(o=2/2) 0.01375
Maintenant, il est écrit P(f >= 0.5) est de 26 %, en hausse par rapport à l'hypothèse précédente de 0,6 %. Donc Bayes nous permet de mettre à jour notre estimation du coût probable de I . Si la quantité de données est petite, elle ne nous dit pas précisément quel en est le coût, mais seulement qu'elle est suffisamment importante pour valoir la peine d'être réparée.
Une autre façon de voir les choses s'appelle la règle de succession. Si vous lancez une pièce 2 fois et qu'elle tombe face les deux fois, qu'est-ce que cela vous dit sur le poids probable de la pièce ? La façon respectée de répondre est de disons qu'il s'agit d'une distribution bêta, avec une valeur moyenne (number of hits + 1) / (number of tries + 2) = (2+1)/(2+2) = 75% .
(La clé est que nous voyons I plus d'une fois. Si on ne le voit qu'une seule fois, ça ne nous dit pas grand chose sauf que f> 0.)
Ainsi, même un très petit nombre d'échantillons peut nous en dire long sur le coût des instructions qu'il voit. (Et il les verra avec une fréquence, en moyenne, proportionnelle à leur coût. Si n des échantillons sont prélevés, et f est le coût, alors I apparaîtra sur nf+/-sqrt(nf(1-f)) échantillons. Exemple, n=10 , f=0.3 , soit 3+/-1.4 échantillons.)
Ajouté :Pour donner une idée intuitive de la différence entre la mesure et l'échantillonnage aléatoire :
Il y a maintenant des profileurs qui échantillonnent la pile, même à l'heure de l'horloge, mais ce qui sort est des mesures (ou chemin chaud, ou point chaud, à partir duquel un « goulot d'étranglement » peut facilement se cacher). Ce qu'ils ne vous montrent pas (et ils pourraient facilement le faire), ce sont les échantillons eux-mêmes. Et si votre objectif est de trouver le goulot d'étranglement, le nombre d'entre eux que vous devez voir est, en moyenne , 2 divisé par la fraction de temps que cela prend. Donc, si cela prend 30 % du temps, 2/0,3 =6,7 échantillons, en moyenne, le montreront, et la probabilité que 20 échantillons le montrent est de 99,2 %.
Voici une illustration improvisée de la différence entre l'examen des mesures et l'examen des échantillons de piles. Le goulot d'étranglement peut être une grosse goutte comme celle-ci, ou plusieurs petites, cela ne fait aucune différence.
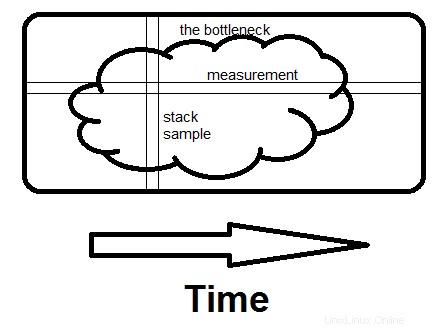
La mesure est horizontale; il vous indique la fraction de temps que prennent les routines spécifiques. L'échantillonnage est vertical. S'il existe un moyen d'éviter ce que fait tout le programme à ce moment-là, et si vous le voyez sur un deuxième échantillon , vous avez trouvé le goulot d'étranglement. C'est ce qui fait la différence - voir toute la raison du temps passé, pas seulement combien.
Vous pouvez utiliser Valgrind avec les options suivantes
valgrind --tool=callgrind ./(Your binary)
Il générera un fichier appelé callgrind.out.x . Vous pouvez alors utiliser kcachegrind outil pour lire ce fichier. Il vous donnera une analyse graphique des choses avec des résultats comme quelles lignes coûtent combien.
Je suppose que vous utilisez GCC. La solution standard serait de profiler avec gprof.
Assurez-vous d'ajouter -pg à la compilation avant le profilage :
cc -o myprog myprog.c utils.c -g -pg
Je ne l'ai pas encore essayé mais j'ai entendu de bonnes choses sur google-perftools. Cela vaut vraiment la peine d'essayer.
Question connexe ici.
Quelques autres mots à la mode si gprof ne fait pas le travail à votre place :Valgrind, Intel VTune, Sun DTrace.