Dans ce tutoriel, nous aborderons l'algèbre vectorielle et les calculs correspondants sous Scientific Linux. Pour notre propos, j'ai choisi Python comme langage de programmation pour sa simplicité et sa puissance de calcul. Toute distribution Linux possède par défaut un éditeur/compilateur Python qui est appelé via une fenêtre de terminal. Passons en revue quelques concepts d'algèbre vectorielle.
Remarque :nous ne travaillerons que sur l'espace réel à deux ou trois dimensions.
Algèbre vectorielle
L'élément d'un espace vectoriel, d'un point de vue mathématique, peut être représenté comme le tableau d'un certain nombre d'éléments appartenant à cet espace vectoriel. Plus précisément, et dans une approche de calcul numérique, il peut être représenté comme une liste de nombres réels, qui a trois caractéristiques de base :
Magnitude
La taille du vecteur et est représentée par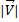 
; il s'agit de la partie scalaire d'un vecteur. Pour calculer la magnitude d'un vecteur, nous devons effectuer la formule suivante :
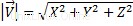
X, Y et Z sont les coordonnées vectorielles.
Orientation
La direction d'un vecteur est donnée par une ligne directrice ayant un angle spécifique pour chaque axe du système de coordonnées appelé angles directeurs.
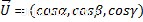
Où alpha, bêta et gamma sont les angles directeurs du vecteur et leurs cosinus sont les cosinus directeurs, ils peuvent également être calculés en divisant chaque coordonnée vectorielle par sa magnitude.
Orientation
Une des deux orientations possibles entre la même direction.
Somme algébrique vectorielle
Pour faire une somme algébrique de vecteurs, il faut additionner les coordonnées homologues de deux vecteurs, ayant les mêmes propriétés de la somme algébrique des nombres réels. Juste comme suit :
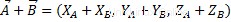Comme nous pouvons le voir, le résultat est un autre vecteur, appartenant au même espace vectoriel.
Produit d'un vecteur par un scalaire
Étant donné un vecteur et un scalaire, le vecteur produit par un scalaire est défini comme le produit scalaire de chaque coordonnée du vecteur :
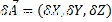
Où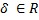 
Vecteur d'unité
Une application directe du vecteur Product par un scalaire est le vecteur unitaire, a vecteur unitaire est un vecteur normé de longueur 1.
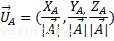
Combinaison linéaire
Lorsque nous mélangeons les opérations passées, somme algébrique et produit vecteur-scalaire, nous obtenons une combinaison linéaire, dans laquelle le résultat est également un vecteur appartenant au même espace vectoriel, comme est :
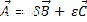
Où le vecteur A est une combinaison linéaire des vecteurs B et C.
Python sur Scientific Linux 7.1
Pour implémenter l'algèbre vectorielle, nous avons choisi Python comme langage de calcul. L'éditeur de texte que nous choisissons est gedit et est fourni par défaut avec la distribution Scientific Linux 7.1.
Magnitude d'un vecteur
Appelons gedit à l'aide d'un terminal ou cliquez simplement sur l'icône dans l'onglet des applications :
Nous devons d'abord travailler avec des listes, comme représentant des vecteurs et doivent être déclarées comme est :
V=[2, 2, 1]
Déclarons une variable pour stocker la magnitude et donner une valeur, nous utilisons 0.
modV=0
Maintenant, nous utilisons les mathématiques de la classe pour exploiter la racine carrée :
import math
Le calcul de la magnitude :
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
Comme nous pouvons le voir, nous devons utiliser des sous-index pour indiquer l'élément de la liste que nous allons opérer, en commençant par 0.
Le script complet est le suivant :
V=[2, 2, 1]
modV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
print (modV)
Une fois terminé, nous devons enregistrer le fichier avec l'extension .py et localiser le chemin du fichier et y ouvrir une fenêtre de terminal avec un clic droit puis "ouvrir dans la fenêtre du terminal". Après nous devons appeler l'interpréteur python en tapant :
$ python [path]/yourfilename.py
cela ouvrira une fenêtre comme celle-ci et donnera le résultat :
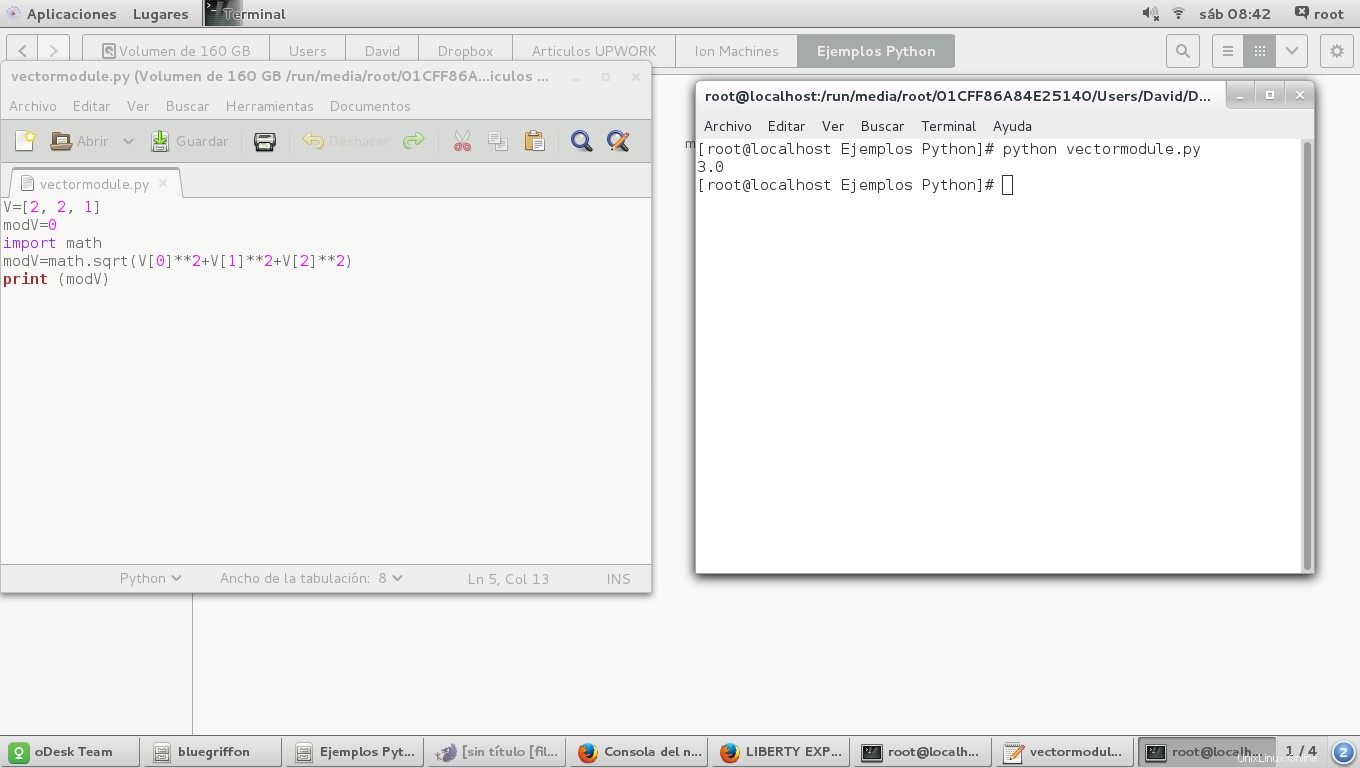
Une autre façon de procéder consiste à utiliser une boucle for comme celle-ci :
for x in range (0,3):
modV+=V[x]**2
modV=math.sqrt(modV)
Ici, nous devons utiliser des techniques d'indentation puisque l'interpréteur Python fonctionne de cette façon.
Direction d'un vecteur
Utilisez les mathématiques de la classe
V=[2, 1, 2]
modV=0
import math
for x in range (0,3): #loop for calculating the magnitude
modV+=V[x]**2
modV=math.sqrt(modV)
for y in range (0,3): #loop for calculating the director cosines
V[y]=V[y]/modV
print (V)
Le résultat est le suivant :
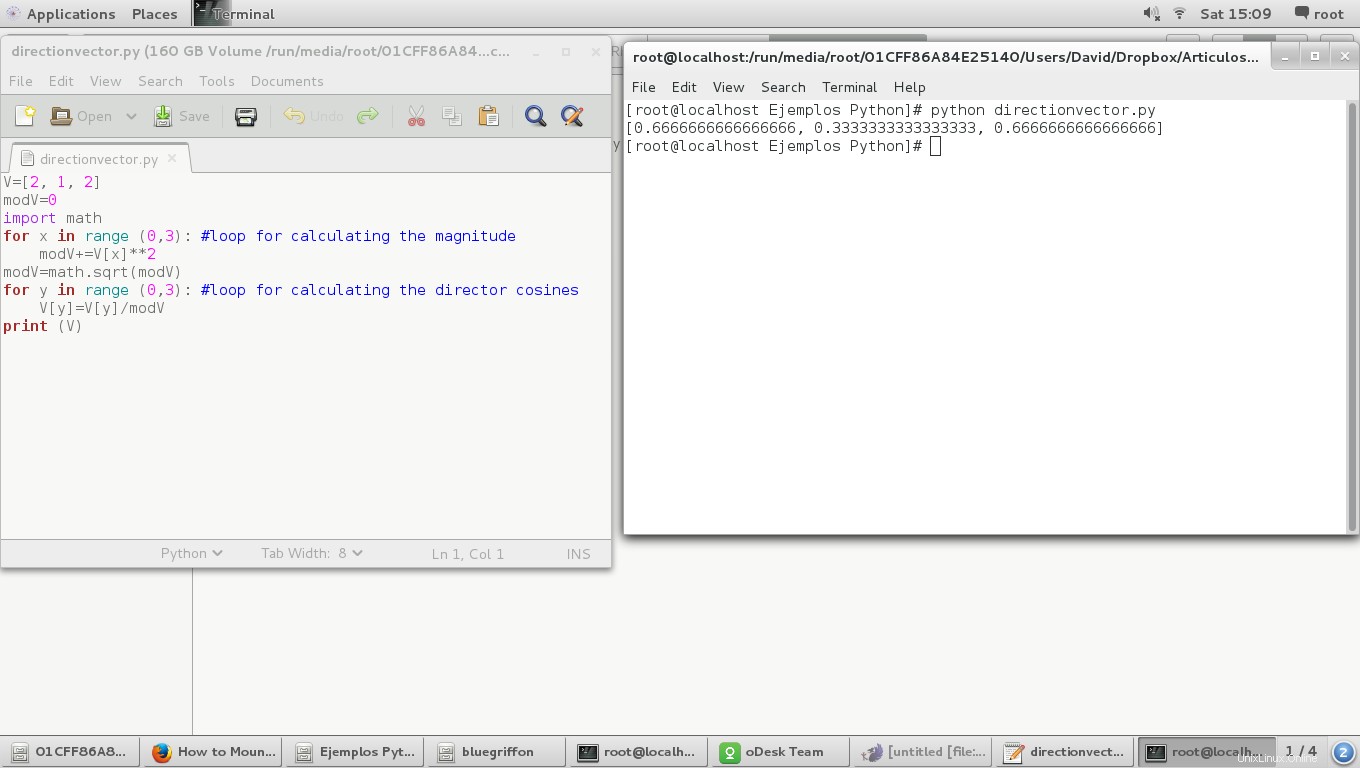
Une autre façon de le faire est d'utiliser les fonctions trigonométriques de la classe mathématique, juste comme ceci :
Commençons par calculer les angles directeurs :
V=[2, 1, 2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))
Et puis calculons les cosinus directeurs et imprimons-les
for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
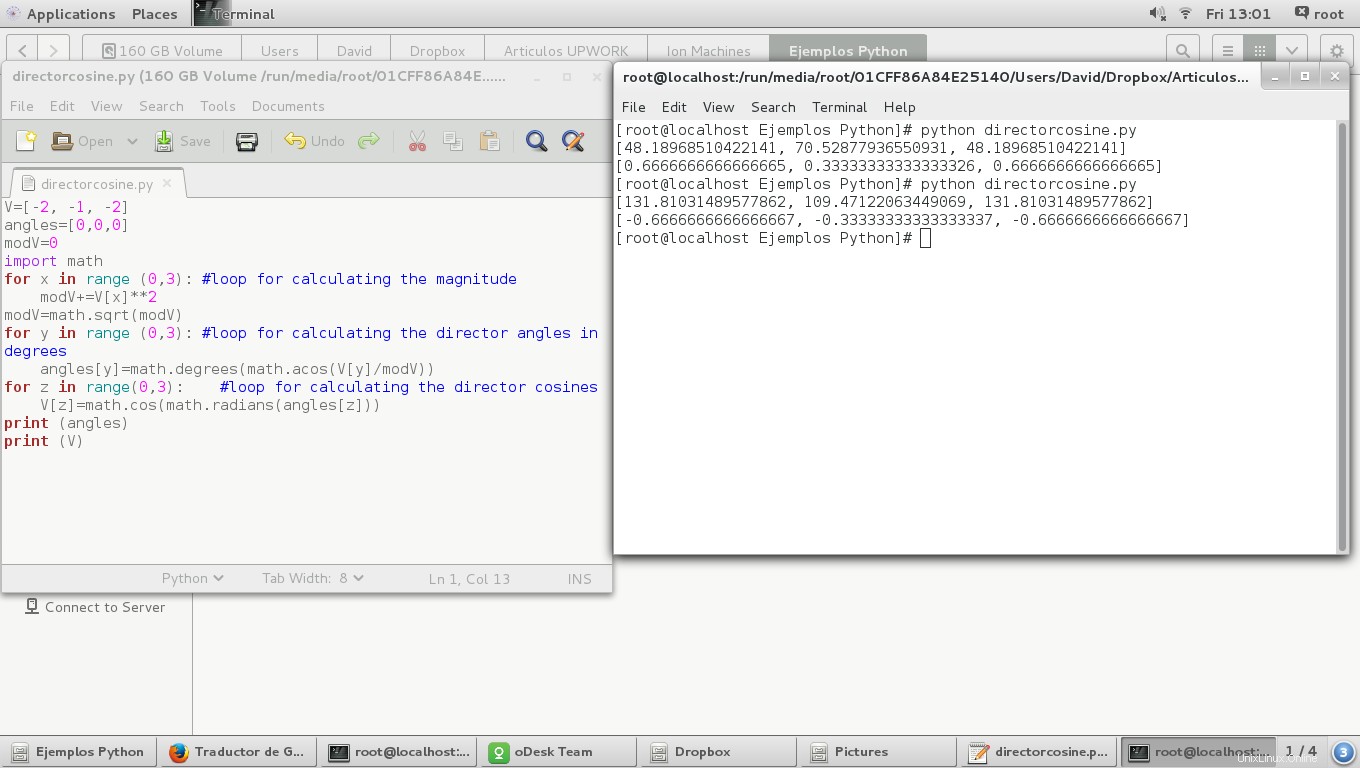
Et le résultat :
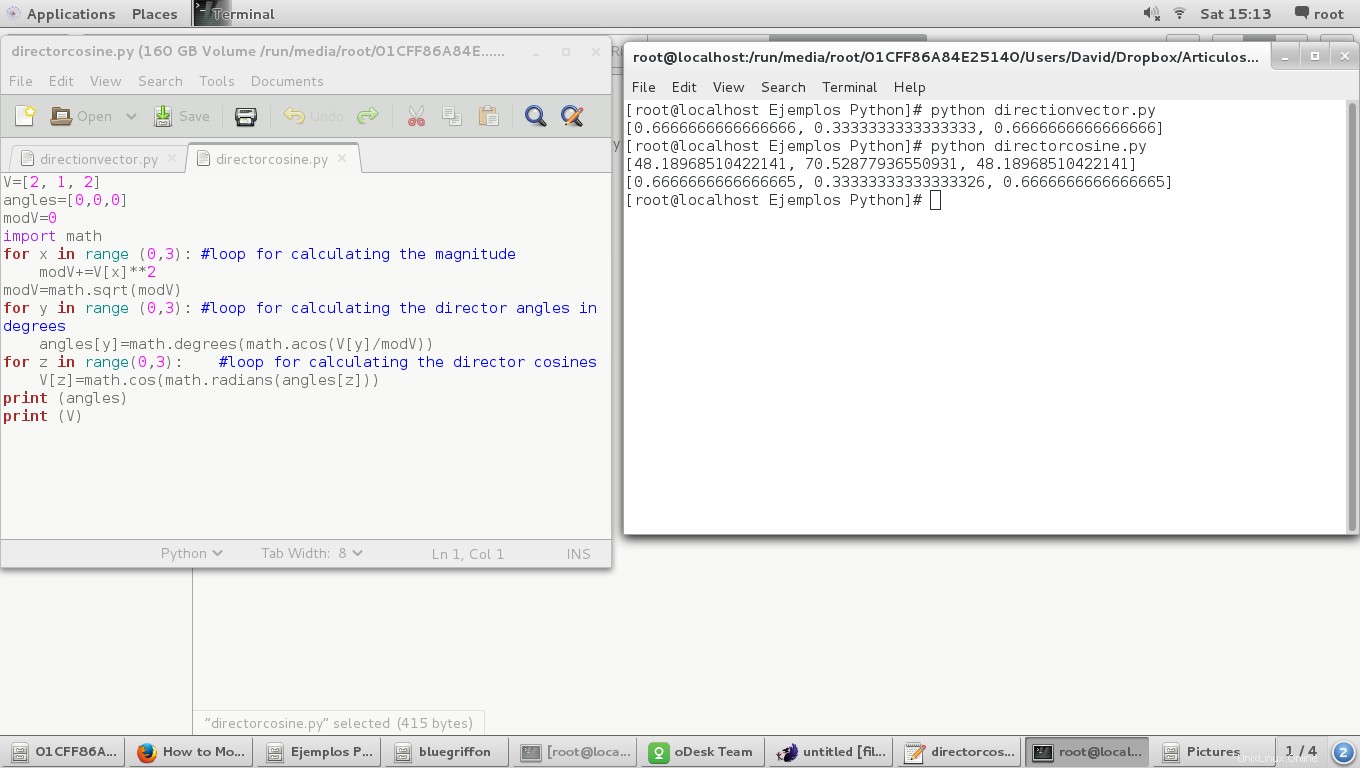
On peut observer que les cosinus directeurs ont la même valeur
Orientation d'un vecteur
Si nous changeons le signe de toutes les coordonnées d'un vecteur, nous modifions intrinsèquement l'orientation du vecteur, tel quel :
V=[-2, -1, -2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
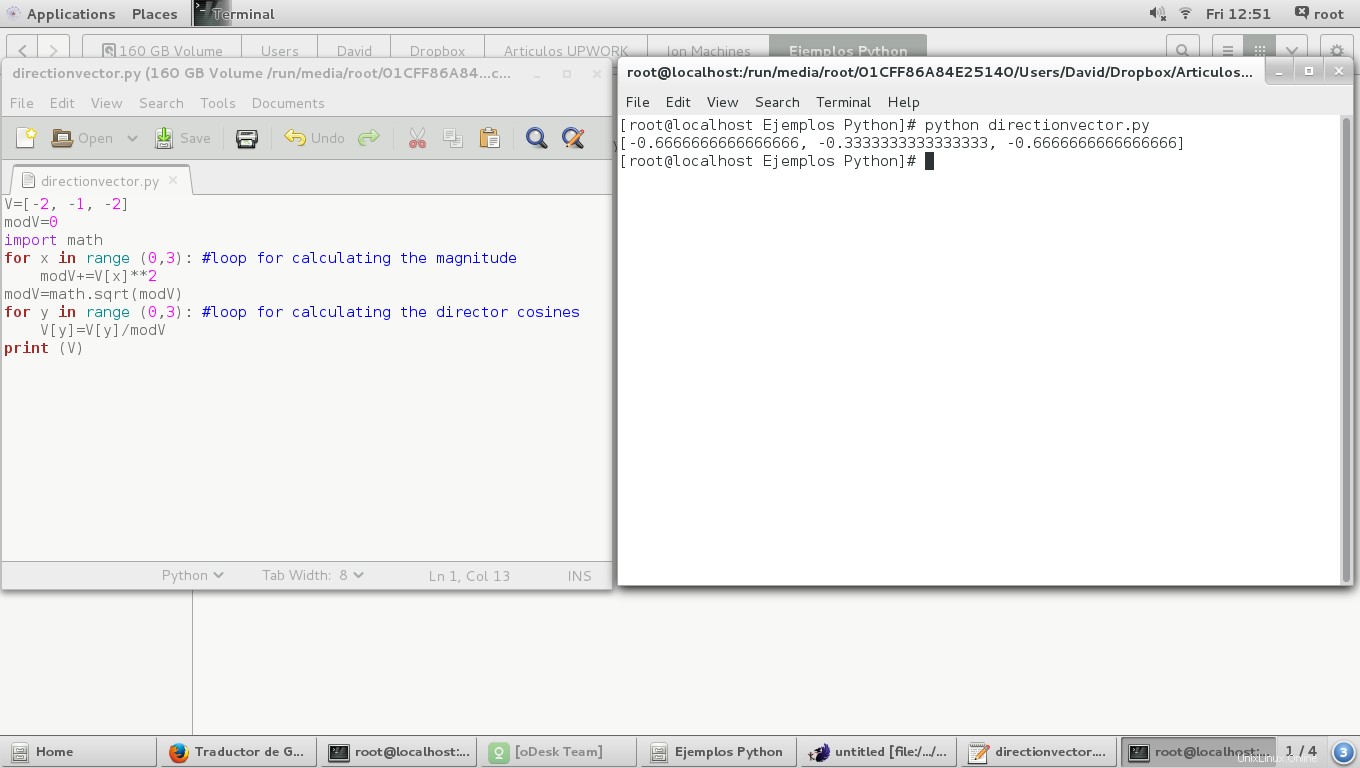
Dans l'image suivante, nous pouvons voir que les angles du directeur sont différents à 180 degrés d'après les originaux
Somme algébrique vectorielle
Nous devons d'abord déclarer tous les vecteurs impliqués dans la somme algébrique, tels quels :
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
où nous allons additionner A plus B et le résultat sera stocké dans S
L'ajout de deux vecteurs (listes) en Python équivaut à exécuter une boucle "for" pour chaque coordonnée du vecteur résultant, nous devons donc faire ce qui suit :
for x in range(0,3):
S[x]=A[x]+B[x]
Ici, nous avons le script complet pour la somme vectorielle algébrique :
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
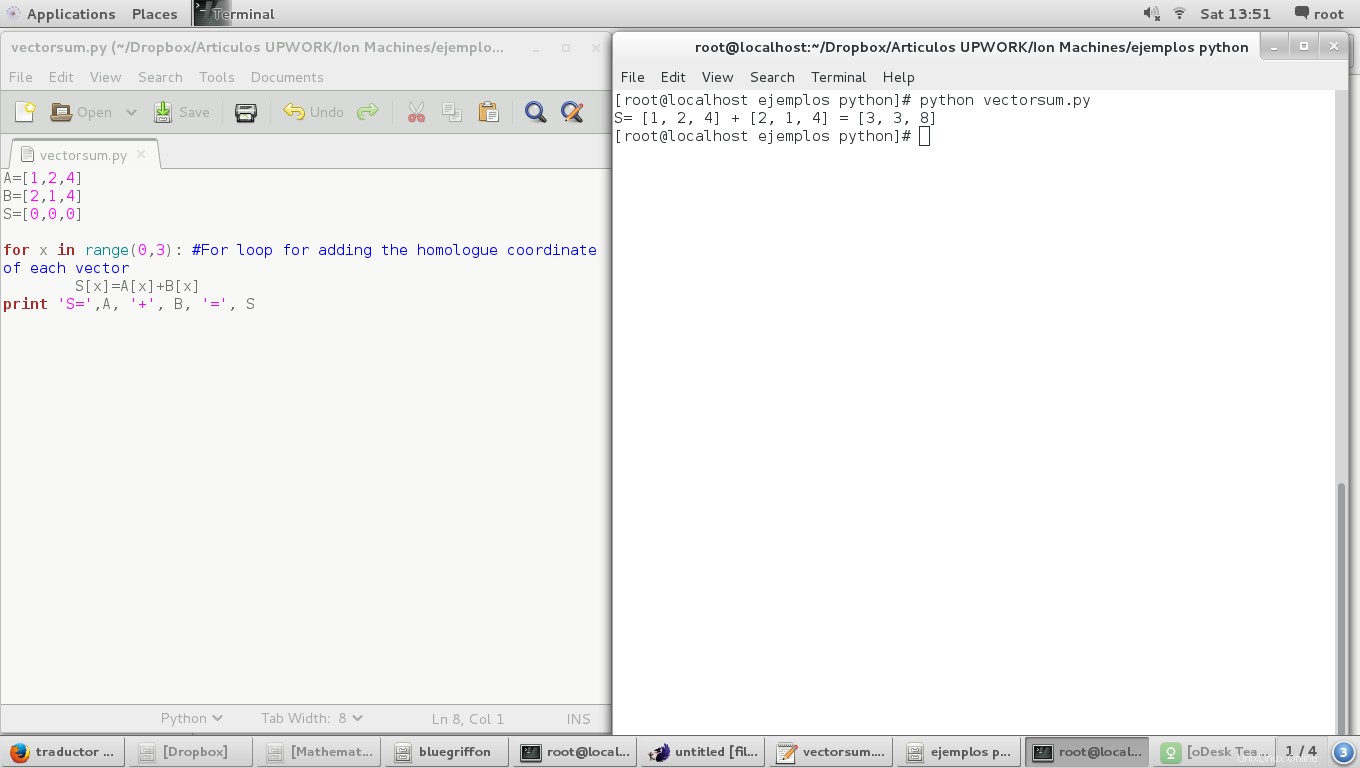
for x in range(0,3): #For loop for adding the homologue coordinate of each vector
S[x]=A[x]+B[x]
print 'S=',A, '+', B, '=', S
Et le résultat est :
Produit d'un vecteur par un scalaire
Étant donné un vecteur :
A=[1,-2,3]
et un scalaire :
scalar=-2
vecteur produit par un scalaire est défini comme le produit scalaire de chaque coordonnée du vecteur :
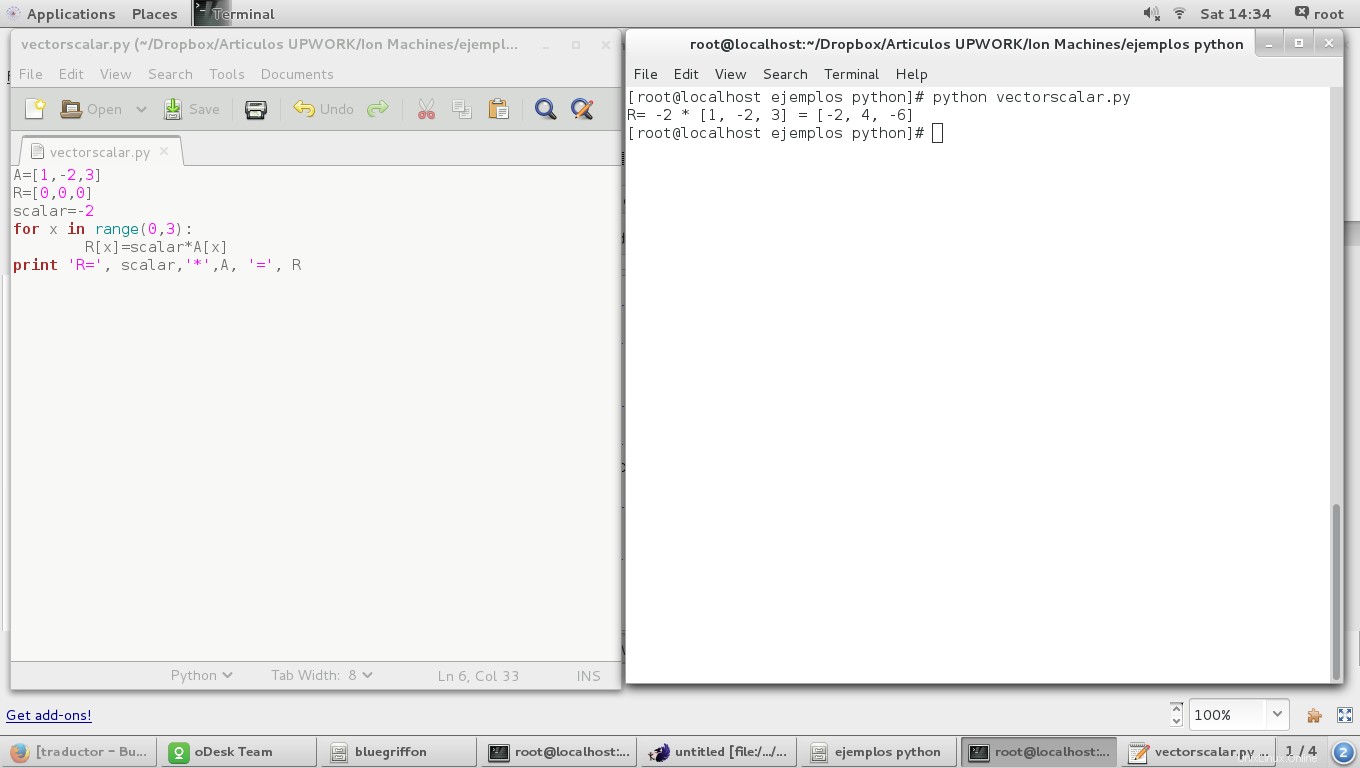
for x in range(0,3):
R[x]=scalar*A[x]
et le résultat est :
Vecteur unitaire
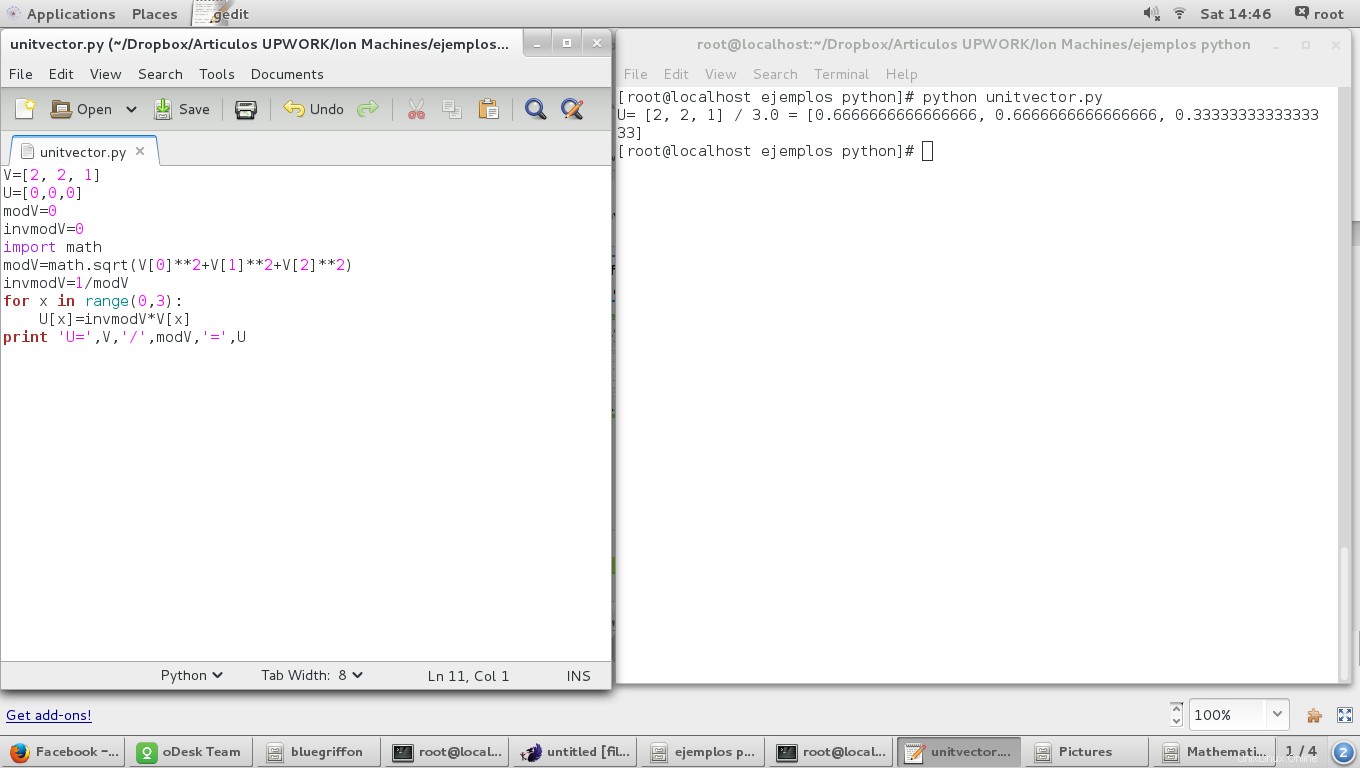
En utilisant le script "Magnitude d'un vecteur", nous avons :
V=[2, 2, 1]
U=[0,0,0]
modV=0
invmodV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
invmodV=1/modV
for x in range(0,3):
U[x]=invmodV*V[x]
print 'U=',V,'/',modV,'=',U
et le résultat est :
Combinaison linéaire
Étant donné trois vecteurs , A, B et C , nous pouvons calculer les valeurs scalaires qui, multipliées respectivement par B et C, donnent le vecteur A. En d'autres termes, placer le vecteur A comme une combinaison linéaire des vecteurs B et C :
A=[7, 9, -8]
B=[1, 3, -2]
C=[-2, 0, 1]
Une combinaison linéaire conduit à un système d'équations , 3 équations à 2 variables ( scalaires ) si trois vecteurs r3 , ou 2 équations à 2 variables s'il s'agit de deux vecteurs dans R3 , que l'on peut résoudre en appliquant un déterminant d'une matrice. Ici, nous devons faire une remarque en raison des types de données gérés par Python. Dans de nombreux cas, lors du calcul des scalaires impliqués dans une combinaison linéaire, le résultat aura des décimales, ce qui entraîne des opérations en virgule flottante. Les types de données numériques, gérés par Python, sont :Integer, Real, Long. Nous devons donc insérer les coordonnées des vecteurs en tant que type de données réel, afin qu'ils représentent des nombres réels (virgule flottante). Nous devons connaître et comprendre certaines caractéristiques du type de données en Python :
- Les entiers occupent moins d'espace mémoire que le type réel.
- Les opérations avec Real sont plus lentes qu'avec Integer.
Ici, nous avons les mêmes vecteurs, mais déclarés de type réel :
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
Ainsi, avec cela, nous pouvons échanger les vecteurs et ainsi toujours avoir la solution du système.
La première vérification que nous devons faire est de savoir s'il y a coplanarité entre les vecteurs ou non, donc savoir s'il y a ou non est une combinaison linéaire. Pour cela, nous allons implémenter une matrice de déterminants :
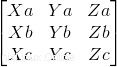
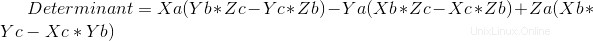
Code :
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
Si ce déterminant est égal à zéro (0) alors il y a une dépendance linéaire entre les vecteurs et on peut continuer à calculer les scalaires. Comme mentionné ci-dessus, le système d'équations a trois équations à deux variables, donnant un système compatible déterminé, pour lequel nous devons prendre deux des trois équations et résoudre des valeurs scalaires, puis vérifier avec la troisième équation, non prise auparavant, si la précédente les valeurs scalaires le résolvent. S'ils ne résolvent pas cela, alors il n'y a pas de combinaison linéaire.
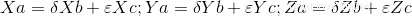
Voici le code complet :
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
if det0==0:
det1=B[0]*C[1]-B[1]*C[0] #First Determinant involving the first and second lines of the equations system
if det1==0:
det2=B[1]*C[2]-B[2]*C[1] #Second Determinant involving the second and third lines of the equations system
if det2==0:
print 'Linear Combination Unexistent'
else:
det3=A[1]*C[2]-A[2]*C[1]
det4=B[1]*A[2]-B[2]*A[1]
sc1=det3/det2
sc2=det4/det2
if sc1*B[0]+sc2*C[0]==A[0]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
det3=A[0]*C[1]-A[1]*C[0]
det4=B[0]*A[1]-B[1]*A[0]
sc1=det3/det1
sc2=det4/det1
if sc1*B[2]+sc2*C[2]==A[2]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
print 'Linear Combination Unexistent'
Et le résultat :
[[email protected] ejemplos python]# python lincomb.py
Scalar 1 = 3.0 Scalar 2 = -2.0
[7.0, 9.0, -8.0] = 3.0 * [1.0, 3.0, -2.0] + -2.0 * [-2.0, 0.0, 1.0]
[[email protected] ejemplos python]#
En conclusion, l'algèbre vectorielle de base se traduit par une série d'opérations impliquant des systèmes linéaires d'équations et/ou de l'arithmétique simple avec des nombres réels. Dans un autre didacticiel, nous verrons comment développer des produits avec des vecteurs, tels que des produits scalaires, des produits croisés ou des produits mixtes.